This long-awaited mod has now been released. There are two versions; a Steam and a WON version. I am currently uploading both to my servers. I will add them as they finish.
“Reissues is a collaborative mapping project that traces its roots back to Project Quantum Leap. The basic idea was to collect a bunch of unrelated maps and short multi-map adventures by authors of all levels of skill, both veterans and newbies, and release it as a single map-pack. There was no story; each map stood (or fell) on its own. The first Issues was the same idea – in fact it was originally called PQL2 – except that it used Spirit of Half-Life as the basis for it’s maps.
Which brings us to Reissues.
Like its predecessors it will be a collection of unrelated maps and short multi-map adventures. It will be based on Spirit of Half-Life. It will not be compatible with Half-Life 2, or Valve’s Source engine. Underneath it all, Spirit is still a Half-Life 1 mod. This is old-school mapping..”
- Title: Reissues
- File Name: hl1-sp-reissues-1.1fix.7z
- Size : 72.7 MB
- Author: Reissues Team
- Date Released: 25 May 2008
Steam Version (V1.1) – Manual Installation
Download to your HDD [72.7 MB]
Steam Version
Important – this archive includes four dll files which should already be present in your Half-Life folder. Only overwrite your existing dll’s if the mod’s ones are newer (very unlikely) otherwise copy only the main Reissues mod folder into your Half-Life folder and leave the dll’s.
- Extract the reissues folder to either your \SteamApps\[username]\half-life or \SteamApps\common\half-life folder (whichever is relevant to your particular Steam installation).
- Restart or start Steam.
- Reissues should now be listed in your Library tab.
If you require more help, please visit the Technical Help page.
This is a collaborative project spanning a wide variety of mapping abilities. Be aware that there may be inherent bugs plus a host of new ones, courtesy of Valve.
Steam Version:
- In Labcoats Required the Scientist stands in front of the retinal scanner, but doesn’t operate it. noclip is required to pass through the door.
- Map Encamped permanently crashes immediately after start with “D_SCAlloc: bad cache width 512”
Click on the thumbnails below to open a medium size image. WARNING: The screenshots may contain spoilers.
Please note: These statistics are valid from December 2010
-
5,075Overall
-
0Today
-
6Last 7 days
-
26Last 30 days
-
288365 days
Using Gauge: Users
Manually: 2 Users
Time Taken:
Average: 4 Hours, 25 Mins
Shortest: 3 Hours, 40 Mins by ꒌ РΔТΔРΣ 14 ꒌ
Longest: 5 Hours, 10 Mins by shaboo
Total Time Played: 8 Hours, 50 Mins
This release is currently not in a collection
If you believe this release is missing important tags, please suggest them in a comment?


































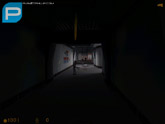
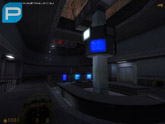



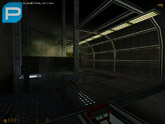







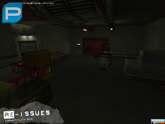




I’m ashamed to say that I started off making a map for this, then I had to give that up, then I was a beta tester for it, then I had to give that up as well (sorry guys – RL got in the way ETC ETC), so if anyone even remembers who I am they probably don’t remember me very fondly…
Having said that, I have nothing but praise for the folks who have seen this all the way through (is it two years in the making now?) and completed (and look like they might soon be releasing) these maps.
I’m not going to give out any spoilers and I know I only played unreleased (and a bit buggy) beta versions quite some time ago; but I will say that there were some seriously top class maps being put together for this map pack.
It will be a testament to what can be achieved by a group of people who have really, really got to grips with the capabilities of HL1 and Spirit of Half Life and have the imagination to utilise those tools in innovative ways.
Let me put it this way: when I played the first collaborative effort from the guys on the Spirit forums (Project Quantum Leap) the stand out map was Adam Foster’s “Someplace Else”. If SE was included in re-issues it really, really wouldn’t stand out as being that special.
I hope this comes out soon – I’m itching to play it!
The article here links to the wrong website; as far as I know, this is the official one now: http://reissues.home.att.net/
Since this has been in “pre-release beta” for the last few months I’ve been eagerly checking every day for its release (as it could possibly be the last great HL1 release). Hopefully things are still going smoothly.
A bit off-topic but can you play Half Life 1 mods with Half Life: Source or is it only with the original Half-Life 1?
I think it’s like “Issues”, HL:Source comes with the pack, you don’t need it installed previously
I believe you need the normal Half-Life. I don’t think any normal mods will work.
Half-Life: Source is not connected to any mod. Perhaps you are confusing it with The Spirit of Half-Life?
Yeah, sry.
I can give a small amount of info on this; Reissues is a mod similar to issues, though not technically a sequel due to the lack of a direct storyline. It is composed of 8 or 9 maps made by various mappers. Each map has it’s own story and are completely unrelated, joined together by a central hub map that you return to after each level to chose a new map. They are currently on the Beta 5 stage and are working out the last bugs and turning in final map builds. My guess is that the beta 6 will soon be available to the beta testers, and the first public release. I will try to give as much info as I can with out giving any spoilers, but as of now I do recommend playing it when the public release comes out.
Yay! Been waiting for this a looong time.
I can’t believe it! It’s finally out! I’m gonna finish it as quickly as possible.
FileFront sucks!! looking forward to downloading it from FileCloud, hope it won’t give me any hard time.
Well, lets say, I’ve played this, few crashing bugs on the Steam version, the WON version runs perfectly. Anyways this mod is something original, very nice gameplay, great level design and so much enjoyable things.
Always will be those maps wich bright more than the others (Like Lost in Time did in Issues), in this case it is the Second Wind mission wich was the most beautiful scenary I’ve ever saw in Half-Life. The others was awesome too, so much, really good mod, play it now!.
No bias in my ratings whatsoever 😀
It’s finally alive! w00! after such a long time.
Kol, let’s just say that I really liked your map. Nice work!
Gonna continue later today.
I noticed that the mod started to crash when I was playing a few chapters, will somebody release a patch soon to correct this?
Hello there,
One of the Reissues team here (“Cyan” is my map). Would like to hear any bugs or issues you have with the mod. Post them up at http://www.chatbear.com/unity2/6189?v=flatold
Like the look of this website by the way. Looks like it’s changed a fair bit since the last time I visited.
There is also a certain sky bug on the chapter It’s Safer Here please fix it.
I find the steam version is very laggy for a HL1 mod.I’ll have to try the won version and see how it is.
It’s Safer Here sky-of-doom bugfix:
r2d2rigo from the Spirit of Half-Life forums found a fix for the It’s Safer Here skybox bug;
1. Start the map.
2. Quicksave.
3. Quickload.
4. Behold! 3D skybox without HOM that makes you wanna go on a killing spree!
Rejoice and thank r2d2rigo.
Hmm… This seens an ambitious project, but I still can’t get enough out of it.
I know it took effort to make, and that the authors joined up and did a good job, with excellent mapping job, in every map of it … Still, as our friend “mel” said in the “Issues” he reviewed, this is an ok project. I wonder if it was different back them, but for me here, probably the HL engine’s just too old to handle these.
Not saying the project is bad either. With a voiceover, this mod is one of the few that actually got a decent job done here. Also, I must state that the WON version I downloaded from the FileCould server, after substituing my HL 1.0.0.8 version hw.dll and sw.dll files, made it stop working. Thanks I had saved it in the desktop and put the originals back on. Wonder if the ones the authors put together there are really neccesary to work?
This mod’s just not perfect for me, because even in the easy setting, it was kind of hard (also it was a stressful day today so I can’t put too much energy playing right now, but that shouldn’t come in case either).
Anyway, one more time, good job and congratulation in your project.
Well, I don’t think so
That’s Looking cool and good.. but
This has too many bugs…
Anyway, I don’t like that, well that’s suXks..
Why don’t fix that?
I had a good fun playing through this project the quality in general is above average and bring us different experience played like small episode that aren’t linked and that you can play in the order you want
For a review just click on my name
Where can I download won version 1.1 or better plus any patch, other then Fileplanet or any other site that wants my money.
@mel, check the DL list above, Phillip has added a FileFront link, just tried it and it works fine!!
Thanks AI, when you say you have checked, do you mean the DL or how the game played? I am having problems with the level I download months ago and was looking for a later version plus any patch. Won version 1.1 seems later then the version I have however, the Filefront down load screen does not state version 1.1 so I’m thinking what I already have was downloaded from Filefrount anyway. Problems I have are; does not recognize map names when trying to load from console, and a helicopter that I am sure I need to get-on just hovering a few feet off the ground.
mel, I think this is newer (1.1) I loaded the WON version and it seems to run very nice as far as I have gone! I don’t think there is a patch for the WON version! This version DL’s at 99.5 mb.
I downloaded the won version from filefront to check and this is from the liblist
game “Reissues”
url_info “http://reissues.home.att.net/”
version “0.5”
size “232144896”
hlversion “1110”
I dunno if he forgot to change the version number or this is an old file.File planet and file front all have the same file listed as 1.1 but I think they are 1.0 as that file is the same size also.I’m gonna try using the steam file in won tonight and see what happens
Question for AI and andyb; have you tried loading a map from the game via the console?
Mel, I tried 2 ramdom maps from the console in Reissues (WON and Steam versions) both ran fine! I don’t know what you need a patch for? My WON version is at 1.1.1.0 and the “Steam” version is whatever “Steam” is!!
OK AI and thanks, I not saying I need a patch just that if there was one I would take advantage of it, one of the above post quoted a pitch. However, I will download the won version from FileFront unless you suggest otherwise, thanks again.
is the sweet half life dll in the half life folder?I believe its sw.dll
Yes it is. I have just downloaded the game again from the above Filefront link and both this level and the other level I had both have the sw.dll. I have not cross checked all the content. However, the new downloaded file is better structured with all the elements in their respective folders, which is not the case with the old download. So something is different. Thanks again andyb.
Ok AI and andyb this is what happens now; I can now load maps from the console but still have the same issue that stop me progressing before, but now I can skip round it by loading the next map.
I maybe missing a trigger; at the beginning of map ‘scepterofra1″ you get your mission info which tells you to get kitted-up and make for the Osprey, but the Osprey is hovering above the ground and you can’t get in it, I have noclip onto the Osprey but still nothing triggers. So have now loaded the next map ‘scepterofra2’, this I am thinking should load if you can get on the Osprey. Any chance in checking this out for me? Either way I am up and progressing again so thanks for all the help.
I’ll check it out in the morning if I have time.Been up since 4am and been working on closing the trailer for the year.Tired now lol.
I manualy loaded the map “Scepterofra1” (WoN version) it loaded fine, got my info, went out to the “Osprey” and had no problem getting in! After I got in the next map loaded with no problem! I’ll try the “Steam” version tomarrow, if you think you missed a trigger point, I don’t know where it is!! Sorry for not being much help to ya!! 🙁
Thanks for checking AI. I just loaded the level again, no change the Osprey is about 20 feet off the ground but the undercarriage wheels are on the ground, crazy. Anyway I have loaded the next map from the console and making progress. Thanks for confirming that the level change was how I expected, i.e. once you get in the Osprey, at least I have not missed anything
I am playing in the portal where I have to recharge the teleporter power supply, when the tank bursts through the wall and I have to find the Rocket Launcher in the “red and green buildings” :-
Well, I can’t even find a red & green building, never mind a rocket launcher.
Anybody help?
Phil
I did look for a red and green building but it didn’t shine at my eyes…I don’t remenber exactly… was it just in the area behind the wall? (recharge are there for sure) or the first building on your right if you let the broken wall behing you or perhaps in the far right corner where there was a tent, explosive box and marine waiting for you when you start…perhaps I had chance but find it without too much searching thats why I don’t remimber right but for shure it’s somewhere in this area 😉
BTW Phillip if you need more screen let me know
The rocket launcher is in an area where you probably already were, among those big square buildings with the catwalks towards the beginning of the map. It’s in a box under a tent that wasn’t open earlier.
Thanks to Stef and Gilfrarry. I did look everywhere for the launcher, but never did find it.
I did kill the tank with grenades though and so managed to continue.
Another question if I may:- I am now in the portal “CYAN” and am stuck again…………….
In a big hall with huge glass windows that look out to desert, there’s a lift in the centre that doesn’t come when called. There’s three floors but I can’t get to the top one (need the lift?) I keep killing all the aliens but they just respawn ’till eventually they kill me. It seems obvious I’m supposed to carry out some predetermined action, (maybe get outside to kill the guy out there that seems to be regenerating the guys inside) but for the life of me I can’t find what it is!
Anybody help?
Phil
The lift takes a long, long time. You can see its progress by the row of lights above it.
Thanks -Gilfrarry — must be more patient in future, and maybe not look for complicated solutions-
Phil
Half of the maps are well desingned, not too much cheating needed. There is no story and some of the maps are buggy. There are new areas to explore.
Reissues has come a long way since it’s beginnings. I think PQL was a good example of amateur mappage, the type of stuff that shouldn’t even be released. There was the odd good one in there (Adam Foster), but the majority was rubbish. Issues was an improvement, but again nothing I’d really want to play a second time, not the type of stuff you’d show off in your portfolio. Fortunately, someone decided to show some quality control with Reissues, because almost everything in it is good quality. Many of the levels are well built, with a variety of styles. Second Wind is obviously the highlight – one of the best, if not THE best looking Half-Life level I’ve seen. It really is about time someone made something of quality that isn’t Lambda corridors and air vents. Or Xen.
I did have some progression problems with some of them, a couple of sequences in Starlabs didn’t appear to initiate, so I had to noclip. Reloads would often crash on Second Wind 2 (I think gman or the sounds had something to do with it). Also I never figured out how to stop the bomb in ra_level2, so I just skipped to the next level.
But anyway, definitely a top-notch set of levels. Congrats guys! Next time I’d like to see no hub, a more consistent theme and proper progression through each level, so each one starts the way the last ended. In other words a seamless episode or 2. And the quality control is a must.
The good thing about this sort of thing is that you don’t have to dedicate five years to making something to release, only 2-3 levels is fine when you’ve got several other mappers contributing as well. If the levels were all released solo then just about every comment would be “too short”, because Half-Life players are so demanding and expect every release to be hours of playtime.
Nearly finished playing this, couple of maps to go, definitely worth the download very good overall. Hated the map EchoTransit, nice idea but i’m a pretty good player and still had to play that about 40 times, half of which were after switching to God mode. By the way to disable the bomb keep hitting the Use key eventually it’ll disappear but the tripwire bombs will remain as they should.
Sky graphic bug in map ItsSaferHere and bug that freezes game at start of map SecondWind can both be solved by switching to OpenGL video mode, at least that fixed them for me. Had problem with screensize later in SecondWind and switched back to Direct3D to solve that. Despite bugs thats my favourite map really fantastic, could have had a few more enemies in it towards the end but still great.
As I said overall definitely worth it, i’m keeping PQL, Issues and Reissues around.
Playing WON version…I am stuck in Second Wind in the “palace” with the shiny floor…The cabinet looks like it should move, but it does not…Is this a known bug?…Other than this glitch, it is an amazing pak…
Salmoneye, I had the same problem with the Steam version. It’s in the big hall where the grunt are fighting aliens, right?
I struggled with it for a foe minutes before I got lucky. You need to push the cabinet from a specific angle, though I couldn’t tell you what that angle is. You do have top be on the left side of the cabinet, and when need to keep your eyes on the floor, since it moves very slowly. Keep trying and you’ll get it.
There’s also a section in a very tall tower that, for me, had a problem with quicksaves – I couldn’t load any, for some reason. I’m curious to know if you have the same problem wtih the WON version – would you mind letting me know?
I just loaded the steam version and you need to push the cabinet through the doorway.You need it for the next part.It moves slowly but it does move.
Wrong place…
After the Gargantua, and the gates that go up and down with the one lever, there is a large Palace Hall with yet another cabinet…
This one does not move, and it is just before map ‘secondwind2’…
It seems I am either missing something, or the cabinet does not move at all…
So far I can not even noclip by it, though there is a video online (in French) where the kid does indeed noclip past this spot…
If you web search this, you can see what I mean:
walkthrough-hlreissues-23
I’ll Try that Darth, and many thanks…
I will also report back if I find issues with anything else,
specifically the ‘tall Tower’…
I’m stuck in the episode where you need to recharge the big teleporter thingie, I just disabled the bomb surrounded with tripwires, then I got on the train and drive the teleporter back inside, and pressed the button to go back down. Then grunts appear from everywhere and start shooting, I don’t even last 3 seconds…..how the HECK to you beat this part ??
This episode is really killing the fun I was having with this mod…
Guess I’ll move forward to that spot later tonight lol.Sorry
No go, Darth…
Have not been able to move the cabinet in the big Palace Hall with the shiny floor…
If I have time this week I’ll load the won version.I found the cabinet you are talking about thou.Took a very,very long time to move it.I didn’t think it was even moving.
It’s a shame that this mod was so buggy, I’ve had problems with both the Steam and WON version. I managed to complete all of the levels and Echo Transit stood out for me, everything about it was great, it even has voice actors!
I did enjoy Second Wind, but there were bugs here too.. the last part was ridiculously difficult as well because you are pretty much stuck standing in one area.
Scepterofra was charming, the Gargantua was hilarious..
With all of the problems I still think that this mod is definitely worth checking out, maybe you won’t have as many problems as I did..
Is there a walkthrough, anywhere? I had to quit Second Wind, and now Echo Transit. The developer website and its forum are no longer.
As a by-product, why I’m playing this and every other half decent or better HL map/mod is there’s nothing to play. All the modders have gone fishing, or ? Its a shame what Steam did as now many of the later mods don’t play, or play properly. Leaving me with HL1 as I have both Steam and Won versions.
I just visited this site again today for the first time in a long time, and couldn’t help but look up the old mods I worked on. I noticed the Reissues website isn’t on this profile, so for completeness sake, here it is (though, admittedly, this site offers better information, I think):
http://reissues.sethorian.net/
I’bve added a link to the site in the Author section of the Basic Details.
Is there any fix for the sound related crashes during the second map of “Second Wind” when loading a saved game? This is really annoying …
Does second wind crash for you right at the beginning? I got around it by playing that part in WON
In general, Second Wind runs fine. Actually, I played the complete mod in HL WON 1.1.1.0 and did not have any bugs or technical problems at all, with one exception: Loading saves during the map “secondwind2” made the game freeze. Fortunately this map isn’t too long, so in the end I played it without loading saves in-between. This is the second time I encountered this problem in a mod (the other mod was “High Speed”), so it would be fine to have a general solution to this.
What a fine collection of nine little mods, providing several hours of gameplay!
Generally I was very impressed by the overall graphics (textures and lighting) and gameplay quality of all mods. Some are just above average, some good, some very good, but there’s no really weak one and I enjoyed them all.
Also I didn’t encounter any bugs or technical problems and never got stuck, with the exception I mentioned above (loading during the second map of “Second Wind” freezes the game).
A strongly recommended quality mod!
Manually
Medium
5 Hours, 10 Minutes
Just today thought I’d have a look at this, but steam can’t load it, just crashes straight away with an error message, seems from the above comments I’m not the only one experiencing problems, but all that aside….how did it get into the ‘Hall of Fame’ ? More bugs than the countryside it seems.
If you want to play HL1 mods I’d recommend to get the WON version of the game, as this is the one most mods are based on. Yes, Reissues has an additional Steam version, but as you can see there are problems with it. Have you studied the installation instructions and read the part about DLLs?
This mod got into the HOF, because it’s great. As I said in my review, I experienced exactly one bug during all nine sub mods.
If this mod is not full of bugs as hell , this would be my favorite Half-Life mod. Idea for mod is great , but they don’t managed to make it good. Some of the maps are great , but some are bad.
Sadly , due to bugs , i can’t play Second Wind 🙁 For me best map is The Scepter of Ra . Only because bugs i will rate this mod 4/5 🙁
Manually
Medium
3 Hours, 40 Minutes
Won’t launch, says it cannot load the reissues/cl_dlls/client.dll . I have checked the reissues folder, and that file is present, and the path specified in the error message is the correct path. Does not say cannot find, says cannot load.
Ideas?
Had the same problem with it not loading the dlls.
Make sure you did this part as laid out in the Installation Instructions:
I just retested this download and the mod runs OK for me.
Did so, it works now, but its incredibly buggy, I keep running into progress stopping bugs.